n-step TD Prediction
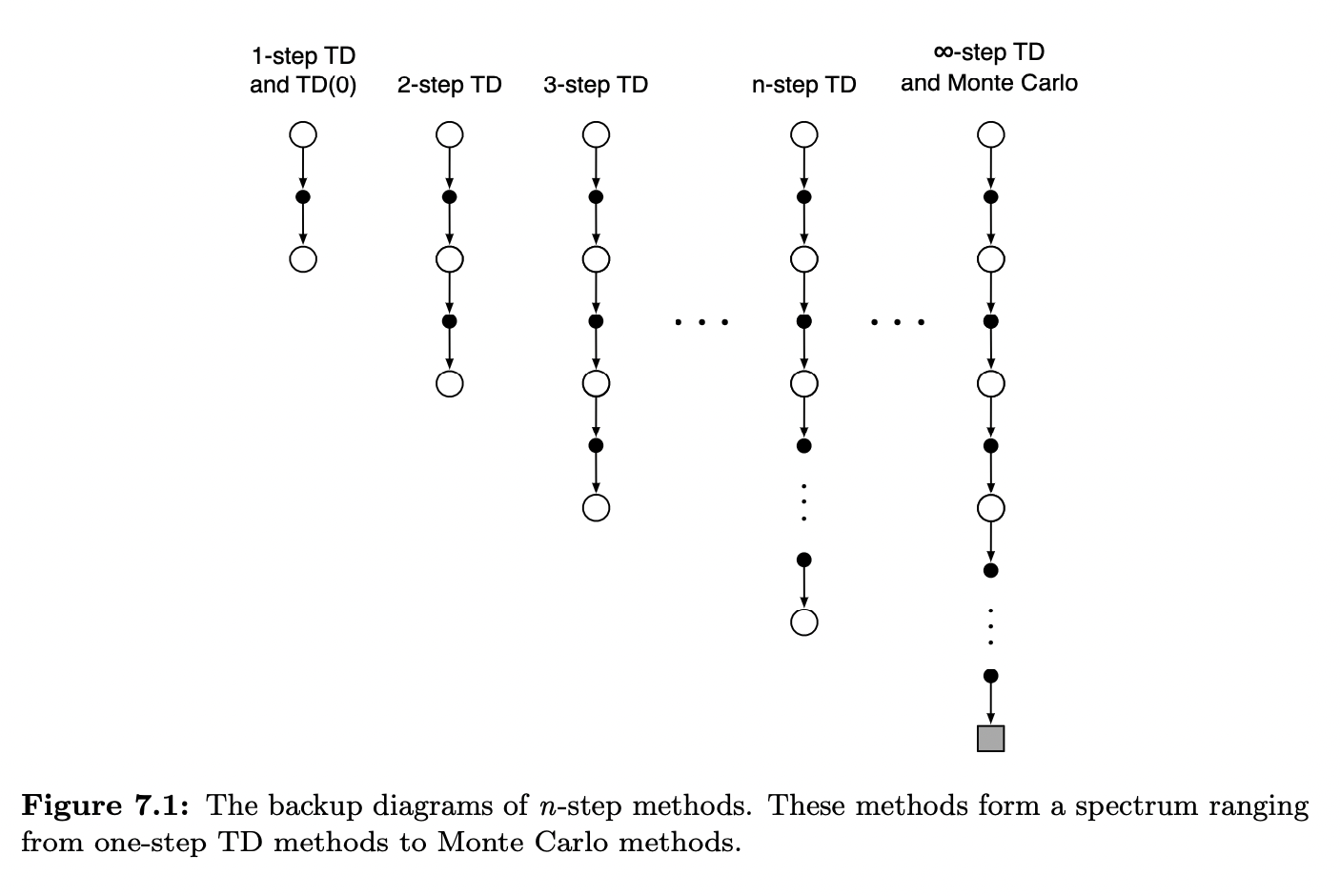
Recall that our one-step return used for TD(0) was:
Gt:t+1=Rt+1+γVt(St+1) we can generalize this to the n-step case as follows:
Gt:t+n=Rt+1+γRt+2+⋯+γn−1Rt+n+γnVt+n−1(St+n) for all n,t such that n≥1 and 0≤t≤T−n. All n-step returns can be considered approximations to the full return, truncated after n steps and then corrected for the remaining missing terms by Vt+n−1(St+n). If the n-step return extends to or beyond termination then all the missing terms are taken as zero.
Pseudocode

The n-step return uses the value function Vt+n−1 to correct for the missing rewards beyond Rt+n. An important property of n-step returns is that their expectation is guaranteed to be a better estimate of vπ than Vt+n−1 is, in a worst-state sense. That is, the worst error of the expected n-step return is guaranteed to be less than or equal to γn times the worst error under Vt+n−1 :
smax∣Eπ[Gt:t+n∣St=s]−vπ(s)∣≤γnsmax∣Vt+n−1(s)−vπ(s)∣ for all n≥1. This is called the error reduction property of n-step returns. Because of the error reduction property, one can show formally that all n-step TD methods converge to the correct predictions under appropriate technical conditions. The n-step TD methods thus form a family of sound methods, with one-step TD methods and Monte Carlo methods as extreme members.
n-step Sarsa
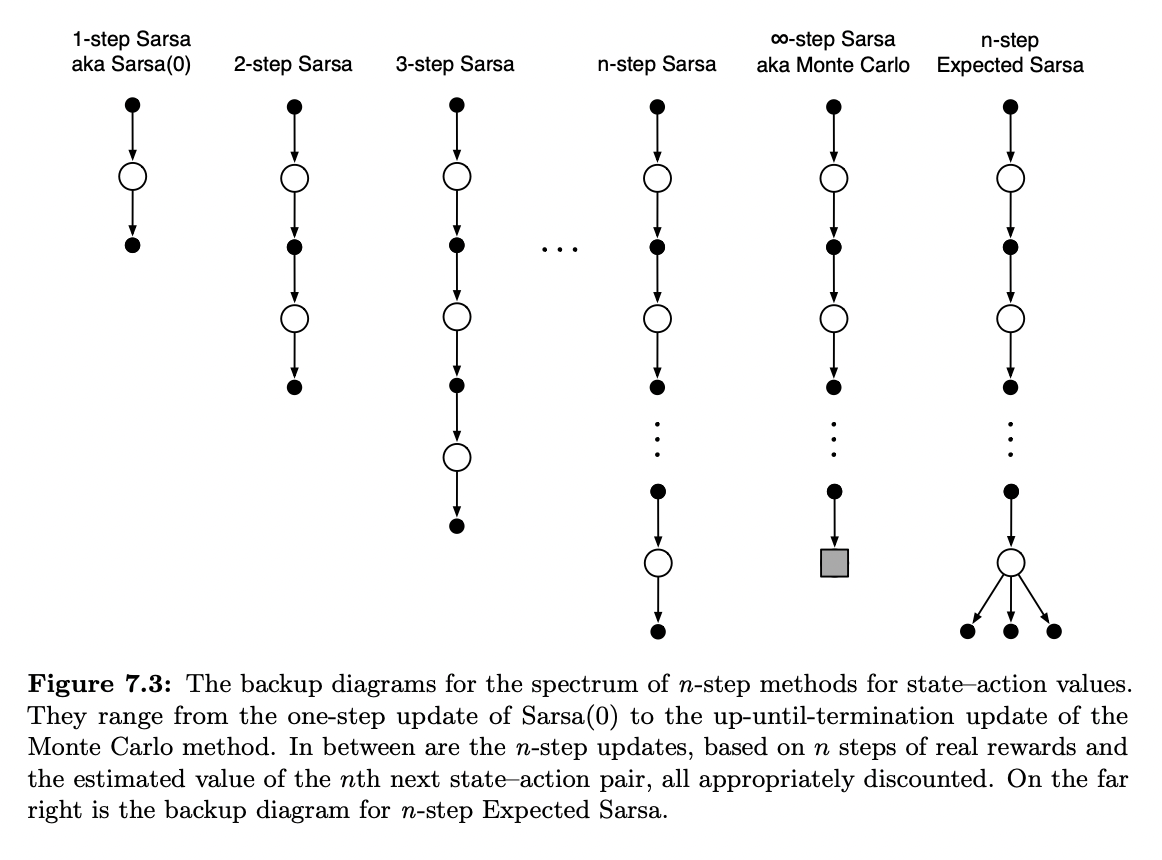
The main idea is to simply switch states for actions (state-action pairs) and then use an ε-greedy policy. The backup diagrams for n-step Sarsa (shown in Figure 7.3), like those of n-step TD (Figure 7.1), are strings of alternating states and actions, except that the Sarsa ones all start and end with an action rather a state. We redefine n-step returns (update targets) in terms of estimated action values:
Gt:t+n≐Rt+1+γRt+2+⋯+γn−1Rt+n+γnQt+n−1(St+n,At+n),n≥1,0≤t<T−n with Gt:t+n≐Gt if t+n≥T. The natural algorithm is then
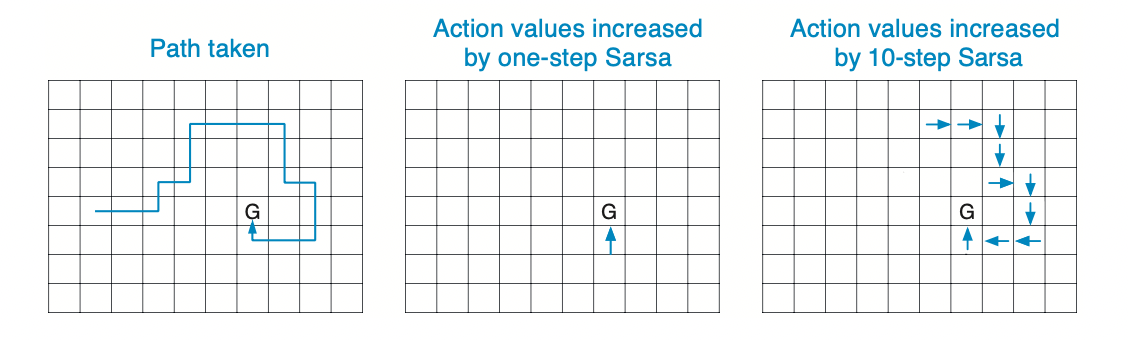
Qt+n(St,At)≐Qt+n−1(St,At)+α[Gt:t+n−Qt+n−1(St,At)],0≤t<T, (7.5) while the values of all other states remain unchanged: Qt+n(s,a)=Qt+n−1(s,a), for all s,a such that s=St or a=At. This is the algorithm we call n-step Sarsa. Pseudocode is shown in the box on the next page, and an example of why it can speed up learning compared to one-step methods is given in Figure 7.4.
Pseudocode

n-step Off-policy Learning
In n-step methods, returns are constructed over n steps, so we are interested in the relative probability of just those n actions. For example, to make a simple off-policy version of n-step TD, the update for time t (actually made at time t+n ) can simply be weighted by ρt:t+n−1:
Vt+n(St)≐Vt+n−1(St)+αρt:t+n−1[Gt:t+n−Vt+n−1(St)],0≤t<T, where ρt:t+n−1, called the importance sampling ratio, is the relative probability under the two policies of taking the n actions from At to At+n−1 (cf. Eq. 5.3):
ρt:h≐k=t∏min(h,T−1)b(Ak∣Sk)π(Ak∣Sk) Pseudocode

Off-policy Learning Without Importance Sampling: The n-step Tree Backup Algorithm
In this tree backup update, the target now includes all rewards plus the estimated values of the dangling action nodes hanging off the sides, at all levels. It is an update from the entire tree of estimated action values. For each node in the tree backup diagram, the estimated values of the non-selected actions are weighted by their probability of being selected under our policy π(At∣St). The value of the selected action does not contribute at all at this stage, instead its probability of being selected weights the instantaneous reward of the next state and each of the non-selected actions at the next state, which too are weighted by their probabilities of occurring as described previously. Formally, the one-step return is as follows:
Gt:t+1≐Rt+1+γa∑π(a∣St+1)Qt(St+1,a) for t<T−1, and the two-step tree-backup return is
Gt:t+2≐Rt+1+γa=At+1∑π(a∣St+1)Qt+1(St+1,a)+γπ(At+1∣St+1)(Rt+2+γa∑π(a∣St+2)Qt+1(St+2,a))=Rt+1+γa=At+1∑π(a∣St+1)Qt+1(St+1,a)+γπ(At+1∣St+1)Gt+1:t+2, for t<T−2.
The latter form suggests the general recursive definition of the tree-backup n-step return:
Gt:t+n≐Rt+1+γa=At+1∑π(a∣St+1)Qt+n−1(St+1,a)+γπ(At+1∣St+1)Gt+1:t+n, for t<T−1,n≥2. This target is then used with the usual action-value update rule from n-step Sarsa:
Qt+n(St,At)≐Qt+n−1(St,At)+α[Gt:t+n−Qt+n−1(St,At)], for 0≤t<T, while the values of all other state-action pairs remain unchanged: Qt+n(s,a)=Qt+n−1(s,a), for all s,a such that s=St or a=At.
Pseudocode







